
Minsait
-
No queremos que nadie espíe o altere las comunicaciones con nuestros bancos, ¡faltaría más! A nivel europeo tenemos ahora la norma PSD2 que obliga a los bancos a abrir nuevos medios de acceso, pero también exige ciertos mecanismos de seguridad.
Quizá estaría bien comprender un poco más que hay detrás de ciertos términos como RSA, clave privada-pública, etc… No hace falta ser informático o matemático para comprender al menos los fundamentos y algunas ideas ingeniosas que se aplican.
Nosotros en minsait y Editran nos dedicamos a eso. Acompáñanos unas pocas páginas y te intentaremos explicar las tripas de todo eso de la seguridad en las comunicaciones digitales. Lo vamos a hacer sobre el modelo de seguridad de Editran, que es el protocolo más usado en España para la tesorería transaccional. Hemos escrito con intención de ser didácticos más que exhaustivos; esperamos que nos perdonen algunas simplificaciones los expertos en seguridad, con los que ya nos pasamos días y días debatiendo cómo hacer las cosas mejor.
Queremos que una comunicación de datos entre dos puntos (tú o tu sistema de gestión y tu banco) sea segura. Esto se desgrana en,
Lo primero es que el software esté bien construido. Hay una práctica cada día más establecida y que nosotros cumplimos a rajatabla que es la revisión por terceros independientes, auditores expertos en seguridad que nos revisan el software y el modelo. En 2019 también el Banco de España revisó el modelo de seguridad con ocasión de PSD2 y lo homologó siempre que los clientes usasen los últimos protocolos de seguridad.
El segundo punto es que el software sólo se vende a empresas, previo contrato, que añade un paso de seguridad. Editran está vinculado al hardware, al ordenador concreto desde el cual se ejecuta. Si intentas cambiar Editran de ordenador, o si alguien intenta simular esa comunicación de Editran desde otro ordenador, no funcionará. Le ponemos muy difícil a un hacker el acceso a Editran para que busque debilidades.
Y el tercero es que cada banco comprueba a quién le da conectividad vía Editran. Los bancos aseguran que se facilita el acceso a una persona con poderes en la empresa y sólo para las cuentas de banco con las que opera esa empresa.
Si juntas todo lo anterior, verás que es muy difícil suplantar o alterar la comunicación atacando Editran. De hecho, no nos ha sucedido nunca. En los últimos veinte años no hemos tenido ni un solo incidente de seguridad.
Con esto hemos resuelto gran parte de la autenticación. Vamos ahora con la confidencialidad, que nadie pueda descifrar las comunicaciones con tus bancos.
Un algoritmo es un método muy bien definido de qué hacer. Y un algoritmo criptográfico es una secuencia de pasos para tratar un mensaje y enviarlo de modo seguro. Cada vez que abrimos el correo electrónico, navegamos por la web, compramos por Amazon o pagamos con tarjeta, nuestras máquinas están ejecutando, incansables, estos algoritmos.
Curiosamente, ya en la antigüedad se usaban algoritmos secretos para cifrar los mensajes, reglas para codificar y decodificar los mensajes que sólo conocían el emisor y el receptor. Se siguió haciendo así incluso hasta la segunda guerra mundial, con la célebre máquina Enigma de los alemanes. Los ingleses capturaron una de esas máquinas, pusieron a un equipo de matemáticos a trabajar en ello, comandados por uno de los mejores de aquella época, Alan Turing, y consiguieron descifrar finalmente las comunicaciones del alto mando alemán con sus espías y tropas. Se dice que fue uno de los factores clave de la victoria aliada.
Resulta que hay un método mejor que encriptar usando un algoritmo secreto: publicar el algoritmo a los cuatro vientos y desafiar al mundo a ver si alguien consigue romperlo (es decir, descifrar los mensajes codificados usando ese algoritmo). Si nadie lo consigue entonces damos el algoritmo por seguro. Hoy existe una comunidad estable de especialistas que pulen los detalles de los algoritmos (criptógrafos) y otros especialistas que emplean todo su ingenio en intentar romper los algoritmos (criptoanalistas). Unos y otros se pasan el día publicando ideas en internet y en congresos, debatiendo entre ellos y puliendo los detalles.
Hay muchos algoritmos seguros posibles. Para la confidencialidad en Editran con PSD2 usamos AES. Para la autenticación RSA. Todo es algo más complicado en la realidad práctica que lo que vamos a explicar, pero sin entrar en ese nivel de detalle intentaremos daros unas ideas de cultura general acerca de AES y de RSA.
El método AES (advanced encryption standard) sale de un concurso que tuvo lugar cerca del año 2000. El NIST, un organismo norteamericano que dicta estándares, lanzó un concurso en la comunidad de criptógrafos para buscar un algoritmo mejor que el DES (data encryption standard), que se llevaba usando en los últimos treinta años y que los criptoanalistas ya eran capaces de romper. Se evaluaron más de una decena de propuestas y se terminan quedando con una de ellas, de dos criptógrafos belgas, Joan Daemen y Vincent Rijmen.
AES es de clave simétrica, que significa simplemente que se usa la misma clave para codificar y para decodificar.
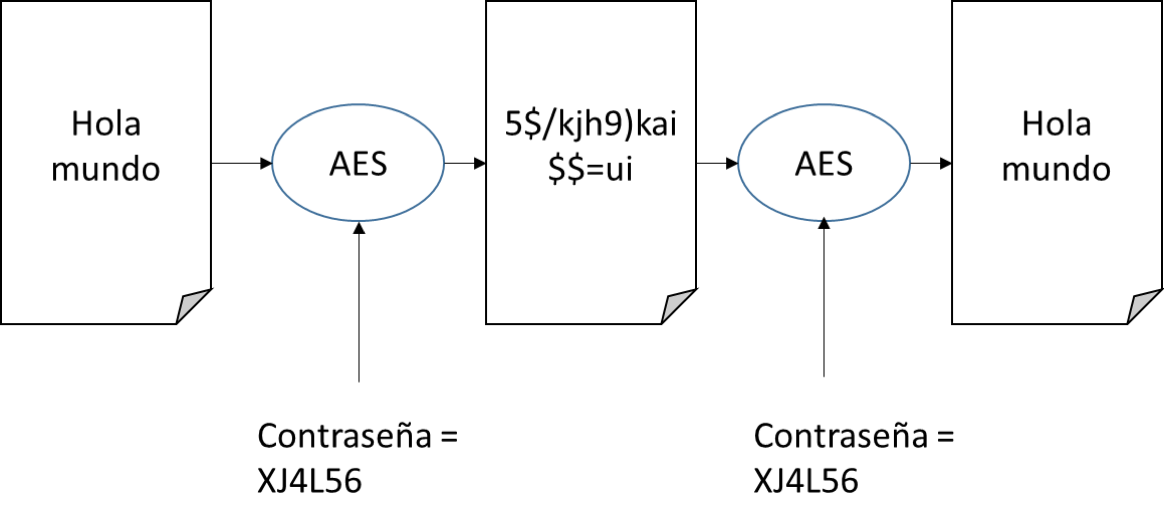
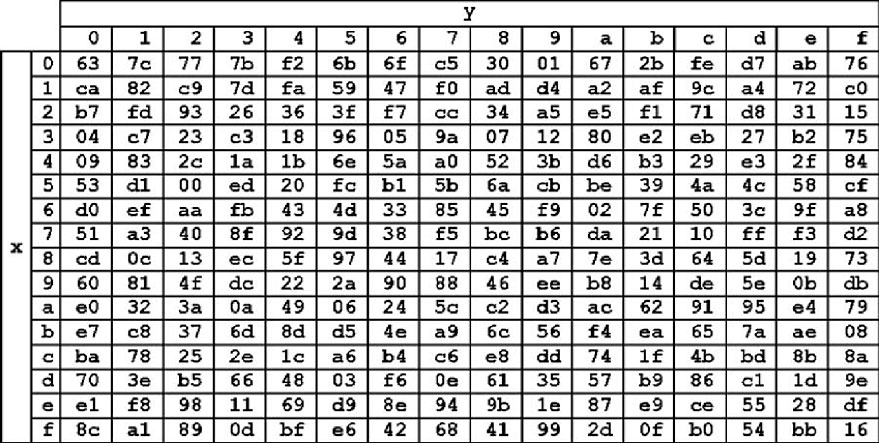
AES se basa en técnicas de sustitución de valores y permutación. La sustitución funciona a partir de una tabla en la que reemplazo un valor de entrada por otro de salida en función de la clave. Es como una tarjeta de claves de un banco donde la sustitución tiene en cuenta la contraseña.
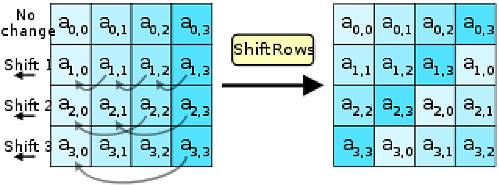
La permutación consiste en cambiar el orden de los datos a nivel de sus bits. Es decir, no cambio un carácter completo por otro, sino los bits que lo componen. Con esto la secuencia ‘Hola’ se puede convertir en ‘&/Uy’ donde el ‘&’ en realidad viene de reagrupar algunos bits de todos los caracteres que hay en ‘Hola’.
Las sustituciones y permutaciones se hacen varias veces en secuencia y los dos criptógrafos las diseñaron cuidadosamente para maximizar el desorden en los datos. En el caso de Enigma resulta que los alemanes comenzaban los mensajes siempre de la misma manera, un saludo con la fecha y el parte del clima. Y las sustituciones se hacían carácter a carácter. Esto fue clave para romper su algoritmo. Con AES todo se mezcla con todo de manera que no haya manera de estudiar patrones en el mensaje codificado por mucha estadística que le apliquemos.
Se usan claves de 256 bits (como passwords de 32 letras), que es muy, muy grande. El número de posibilidades es 2^256 (2 multiplicado por sí mismo 256 veces). Aquí toca recordar la leyenda del ajedrez
https://es.wikipedia.org/wiki/Problema_del_trigo_y_del_tablero_de_ajedrez
Un rey le ofreció al sabio que inventó el ajedrez que pidiese lo que quisiera. El sabio le dijo que un grano de trigo en la primera casilla, dos en la segunda, cuatro en la tercera, ocho en la cuarta y así en secuencia.
Este cálculo da un número muy grande muy pronto. ¡Para llenar así 64 casillas hace falta la producción mundial de trigo durante un milenio! Pues con los cuatro tableros de ajedrez que hay en 256 casillas el número que sale tiene 77 dígitos en notación decimal, que es del orden del total de átomos que se calcula que hay en todo el universo. Es decir, si uno se pone simplemente a probar claves puede tardar una eternidad en acertar con la correcta. Y la sustitución y permutación lo desordena todo de manera que no se puedan ver patrones en los datos codificados.
Si quieres profundizar un poco más, una buena explicación:
https://www.youtube.com/watch?v=tzj1RoqRnv0
Hoy se considera AES seguro, incluso para codificar información de alto secreto de las agencias gubernamentales de seguridad o en comunicaciones militares. Es decir, es muy seguro y lo usamos todos los días en Editran para asegurar la confidencialidad de los mensajes entre editran y los bancos.
RSA se usa, por ejemplo, en la firma electrónica. Los certificados de la FNMT y cualquier otra entidad se basan en RSA. RSA se usa también en PSD2 para todo lo que tenga que ver con autenticar a uno de los extremos.
RSA viene del nombre de los tres matemáticos que lo inventaron en 1979, Rivest, Shamir y Addleman. Aplicaron ideas en las que se llevaba trabajando décadas aplicando matemáticas del sXVII, de dos genios como Euler y Fermat. Son matemáticas sobre propiedades de los números y concretamente de los números primos.
El truco que usa RSA es de una inteligencia apabullante, en opinión del que escribe, de lo más sofisticado que ha conseguido la mente humana. Lo que sigue es una explicación muy simplificada e imprecisa. A todo el que le interese y tenga un corazón un poco friki le recomendamos sin dudas que estudie en profundidad cómo funciona.
RSA se basa en dos principios,
Con las claves simétricas que vimos antes en AES hay un problema. La seguridad se basa en que sólo el emisor y receptor conozcan la clave. ¿Cómo hacen para intercambiarla la primera vez sin que nadie se entere? Si lo hago por email en realidad dependo de la seguridad del email, que no es mucha. ¿El teléfono? ¿Whatsapp? Ejem…
¡En realidad lo que sucede es que el método seguro, el que los humanos damos por bueno, es vernos cara a cara y pedirnos el DNI! Y aun en esto, un DNI se puede falsificar, pueden ponernos micrófonos y cámaras, etc… pero quedémonos en el principio de que un método de cifrado es tan bueno como sea el intercambio inicial. Ahora entenderéis mejor todo lo que hacen los bancos con el bastanteo de poderes para dar acceso a emitir pagos desde una cuenta de banco.
Hay una manera mejor… Asimétrica quiere decir que hay dos claves, una pública y otra privada. La forma más fácil de entenderlo es con la analogía de candado y llave. Al candado lo llamamos la clave pública y a la llave que lo abre, clave privada. Imaginad que quiero cifrar los mensajes que me llegan. Puedo entonces comprar muchos candados iguales y distribuirlos abiertos por el mundo y quedarme con la llave. Si alguien quiere enviarme un mensaje lo mete en una caja, la cierra con uno de mis candados y me la envía. Sólo yo tengo la llave y sólo yo puedo abrir la caja. Así funciona RSA. Creamos una clave, enseñamos a todo el mundo la clave pública y nos guardamos la privada.
Las claves asimétricas solucionan un problema que había de siempre en las claves simétricas de cómo intercambiar las contraseñas. Con la clave asimétrica se resuelve ese problema porque la clave privada no se publica y puedo enviar mensajes seguros sin necesidad de intercambio inicial de claves.
RSA sirve para cifrar mensajes, pero también para autenticar. Resulta que la codificación con clave pública y decodificación con clave privada funciona también al revés. Puedo codificar un mensaje usando la clave privada y se puede decodificar con la clave pública. Así, si publico mi clave pública y después codifico algo con mi clave privada, cualquier puede decodificarlo con mi clave pública y saber que fui yo el que envió el mensaje. Así funcionan hoy los esquemas de firma digital.
En lo que decíamos antes de RSA y clave asimétrica, cuando distribuimos el candado (clave pública), no queremos que nadie pueda llegar a la llave (clave privada) a partir del candado. Esto se consigue en RSA jugando con algunas propiedades de los números primos, que son los números naturales mayores que 1 y que solamente son divisibles entre sí mismos y el 1.
Imagina que tomamos dos números primos y los multiplicamos. 3x7=21 Y te pido que encuentres los factores. Bueno, el 21 nos lo sabemos, pero lo que harás en general es,
Es decir, para factorizar un número vas comprobando si es divisible entre números primos cada vez mayores (2, 3, 5, 7, 11…). Si llegas en este proceso hasta un número primo superior a la raíz cuadrada del número que quieres factorizar, puedes dejar de buscar: el número no se puede factorizar (es decir, también es primo).
Cualquier número natural se puede descomponer en sus factores primos. Factorizar es el proceso de encontrar estos “componentes” de un número dado, y sabemos que es difícil porque los mejores matemáticos llevan siglos intentando, sin éxito, encontrar un algoritmo eficiente para conseguirlo.
Lo anterior quiere decir que hacer 3x7=21 es fácil pero el camino inverso (encontrar 3 y 7 a partir del 21) se complica para números grandes. Cuando se usan números primos muy grandes, que no son difíciles de generar, resulta que hacer la factorización le puede llevar a un ordenador muy potente trillones de trillones de años.
Entonces imagina que usamos el 21 como clave pública y me guardo el 3 y el 7 como clave privada.

La realidad es más complicada de lo que muestra la imagen. La codificación y decodificación en RSA se basa en divisiones y cálculo de restos de divisiones, usando matemáticas ya antiguas que se llaman ‘aritmética modular’. Son trucos con los números que parecen mágicos hasta que los estudias. Una explicación más profunda y precisa de esto:
https://www.youtube.com/watch?v=CMe0COxZxb0
Animamos a todos a ver esto con calma, aunque avisamos de que aquí ya te hará falta algo de facilidad con las matemáticas, lápiz y papel y un cierto tiempo para pillarle el truco.
RSA se considera seguro si se usan claves (números) grandes. Hoy la recomendación es usar claves de 2048 o 4096 bits, números del orden de 2^4096, que son gigantescos. Si 2^256 era grande, imaginad el 2^4096. A cualquier ordenador le resulta fácil generarlos, pero ni el ordenador más potente disponible, el mejor que pueda tener Google, IBM o la NSA, es capaz de factorizarlo en menos de trillones de años.
Es decir, esto de la factorización de los números primos te da un camino no reversible. Es fácil ir hacia adelante con las claves, pero poco menos que imposible en el otro sentido. Por eso puedes publicar tu clave pública de tu certificado de la FNMT con la seguridad de que nadie podrá llegar a tu clave privada.
Hay una novedad interesante en todo esto. Ya se ha diseñado un método para romper RSA con ordenadores cuánticos. Pero parece que vamos a tardar todavía tiempo en conseguir que esos ordenadores cuánticos funcionen de verdad en la práctica así que RSA es seguro a todos los efectos.
Esta es la parte más fácil. Imagina que te envío un mensaje y al final le añado una suma. Me explico: le doy a cada letra un valor numérico y al terminar el mensaje le añado la suma de los valores.
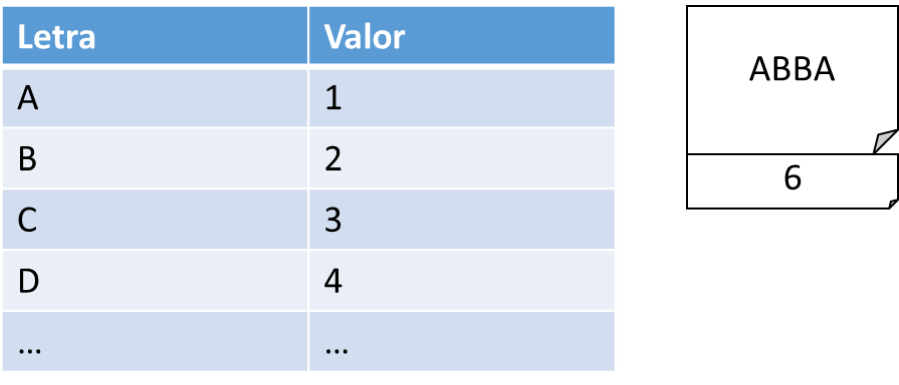
Es lo que se llama un “Hash”. Si en medio alguien cambia una B por otra letra (o hay un ruido en la comunicación), al recibir y comprobar la suma sabré que algo ha ido mal. En la práctica es algo más complicado pero el principio es este.
La norma PSD2, además de definir nuevas maneras de interactuar con los bancos, fija requisitos mínimos de seguridad. A estas alturas todos conocemos ya SCA, la autenticación fuerte de clientes.
Significa que hay que ejecutar al menos dos de tres métodos de autenticación,
En el caso de Editran, y siempre que se actualice el sistema a los protocolos modernos AES y RSA, el Banco de España dio por válido el modelo de seguridad bajo PSD2 sin necesidad de hacer SCA en cada transacción.
No obstante, el Banco de España, y nosotros, recomendamos que se use adicionalmente la firma electrónica. Además de añadir otro punto de seguridad, daría tranquilidad a los tesoreros sobre el envío de remesas a sus bancos. Y los bancos tendrían también la verificación de que una persona con poderes ha firmado la remesa.
Si has llegado hasta aquí esperamos haberte ayudado a comprender un poco mejor este que ya es nuestro día a día. Felices y seguras comunicaciones digitales.